Â
New Chart Display Capabilities in LINGO:
The Network Chart Type can display charts of networks. Multiple networks can be displayed on a single chart.
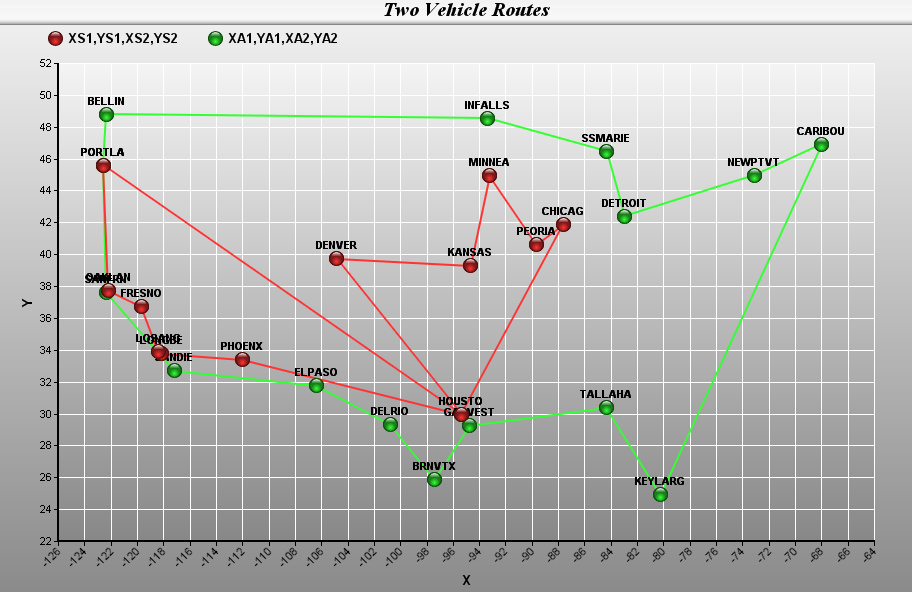
Easy generation, e.g., two or three statements, of graphs of functions, e.g.
Permuted Matrix Displays:
You may now choose to have a model's underlying matrix displayed in a variety of orderings. Here for example is the display of a model in its original ordering:
Here is the same problem with rows and columns permuted with just a click into block-triangular format. If a matrix has good block-triangular structure, then the model is likely to perform well when solved with the new Branch-and-Price solver.

Faster Rendering of Matrix Displays:
For models with more than 10,000 variables or constraints, the speed of rendering of the display has been improved by several orders of magnitude.
Dynamic/Programmatically Derived Sets in LINGO:
The @INSERT function has been added, which allows the dynamic addition of set members to derived sets. This is handy for applications in which the definition of a set of objects is complicated.
Procedures/Public Subroutines in LINGO:
LINGO now supports callable procedures. Callable procedures are similar to CALC sections, however, unlike CALC sections, procedures may be called and executed multiple times.
Numerical Integration Function:
There is now a simple command, @INTEGRAL( ), for computing the numerical integral of a function over an interval.
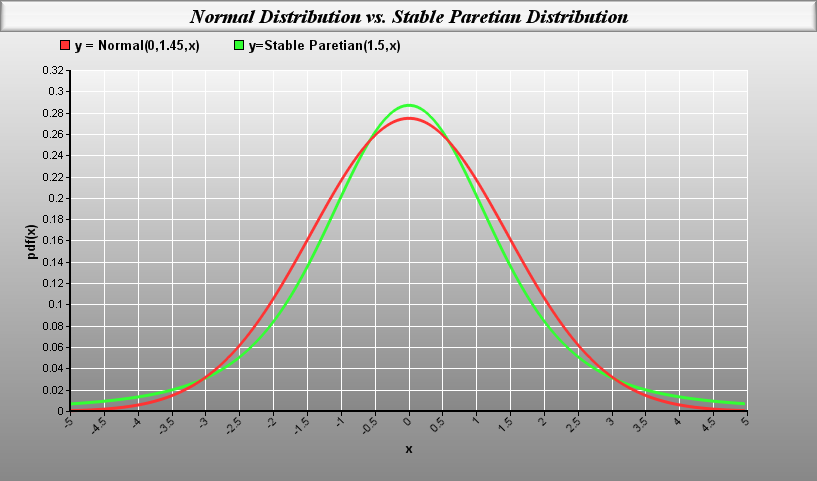
More Probability Distributions Available for Planning Under Uncertainty:
The Beta-Binomial and Symmetric Stable distributions have been added to the list of supported distributions. Stochastic programming models may also specify random variables as having either a Beta-binomial or Symmetric Stable distribution. The Beta-Binomial is useful in Bayesian analysis involving the Binomial distribution, e.g., in designing sampling plans for new drug trials. The Symmetric Stable is sometimes used to model the movement of prices in financial markets.
Date and Time Functions:
A number of new functions have been added to convert dates to and from scalar time, where scalar time is defined as the number of seconds since midnight 1 Jan 2000. These functions are helpful when you need to perform date arithmetic in your models. Among other things, these functions are useful for answering questions of the form, "If the my flight leaves Chicago at 10:30 am on June 21 and the flight to Beijing takes 13 hours, what will the date and local time be in Beijing when I land, and will I be able catch a local flight at . . .?".
Reduced Solve Time on Multi-core Machines:
LINGO 14.0 and What’sBest! 12 can take advantage of computers with multicore processors. The multicore extensions are of two types: concurrent and parallel. Concurrent algorithms run two or more different serial algorithms on multiple copies of the same model, using a separate thread for each algorithm, terminating as soon as the winner thread finishes. Parallel algorithms, on the other hand, parallelize computationally intensive portions of the serial algorithm to distribute the workload across multiple threads. Solvers with multicore extensions include Barrier, Global, Integer, Linear, Multistart and Stochastic.
Reduced Model Generation Time on Multi-core Machines:
In addition to the solvers, LINGO's model generator has also been extended for multicore support. Model generation times for large models can be reduced up to as much as 50% when compared to previous releases.
Branch-and-Price Solver:
A new Branch-and-Price solver with multicore support has been added for improved performance on problems with block structures. Detection of decomposition structures has also been improved in support of the Branch-and-Price solver.
MIP Solver Improvements:
The solution finding heuristics have been improved significantly. Simple rounding and the feasibility pump now use bound propagation to improve the current path to a new feasible MIP solution.
New polishing heuristic to improve the best MIP solution using a pool of previous obtained MIP solutions and the current relaxation. This leads to better MIP solutions faster on many problems.
Multithreading can lead to speed improvements from 1.5 to 3.0 times on difficult problems using 4 threads rather than 1. For easy MIP problems, e.g., < 600 seconds, multithreading may give not much speedup.
Multistart Solver Improvements:
The Multistart solver has been improved significantly, achieving speed factors up to 2X compared to the previous version. The likelihood of getting the global optimum has also improved by 10-15% over a wide range of nonconvex models.
Multithreading often leads to speed improvements from 2.0 to 3.0 times when using 4 threads. Speed improvements tend to improve as the model size and the number of multistarts increase.
Global Solver Improvements:
A parallel algorithm has been added for exploiting multicore machines.
